The Golem Project Automatic Design and Manufacture of Robotic Lifeforms Hod Lipson and Jordan B. Pollack

Simulator

Both the mechanics and the neural control of a machine were simulated concurrently. The mechanics were simulated using quasi-static motion, where each frame of the motion is assumed to be statically stable. This kind of motion is simple to simulate and easy to induce in reality, yet is rich enough to support various kinds of low-momentum motion like crawling and walking (but not jumping). The model consisted of ball-joined cylindrical bars with true diameters. Each frame was solved by relaxation: An energy term was defined, taking into account elasticity of the bars, potential gravitational energy, and penetration energy of collision and contact. The degrees of freedom of the model (vertex coordinates) were then iteratively adjusted according to their derivatives to minimize the energy term, and the energy was recalculated. Static friction was also modeled. The use of relaxation permitted handling singularities (e.g. snap-through buckling) and under-constrained cases (like dangling bar). Noise was added to ensure the system does not converge to unstable equilibrium points, and to cover simulation-reality gap. Material properties modeled correspond to the properties of the rapid prototyping material (E=0.896GPa, r=1000Kg/m3 Syield=19MPa). The neural network was simulated in discrete cycles. In each cycle, actuator lengths were modified in small increments not larger than 1 cm.

Simulator physics

Static solution of each frame is achieved by defining a global system energy term H and then slightly modifying each of the systems degrees of freedom so as to lower H according to its partial derivatives. This process continues until relaxation is reached or instability is determined. The terms included in H define the richness of the simulation.
For example, a basic model including bar flexion and gravitational energy would be:

where n is the number of bars, and for each bar i, m represents the mass, h represents the average height, and the term k represents the stiffness,

where E is the material's module of elasticity, A is the cross section, and l is the length of the bar, and d represents the difference between the bar's current length and its original length, given by

and v,w represents the two current endpoints of the bar. Differentiating the total energy H with respect to each of the degrees of freedom (coordinates of the endpoints, in this case), produces direction of adjustment (second derivatives would produce a more accurate adjustment, etc.).

where Ds (the relaxation factor) represents the adjustment magnitude for each iteration. Each degree of freedom is then updated by its adjustment value, and H is recalculated. Small Ds produce a stable but slower convergence, whereas large Ds can solve static frames faster but may run into stability problems. This process is repeated until adjustments go below a certain threshold.
Although this solution method is slower that simultaneous solutions, (e.g. finite elements), it is capable of solving correct highly-nonlinear cases (e.g. contact collision and snap-through buckling) and, more importantly, under-constrained states: for example, a truss in mid fall which is not yet fully supported (by six rigid-body equations), as it falls into position. Indeed as machines move and function within the simulator they often pass through such stages. As additional real-world energy terms are added to H, it becomes more accurate. We have included terms for friction, collision between bars, external forces and noise.

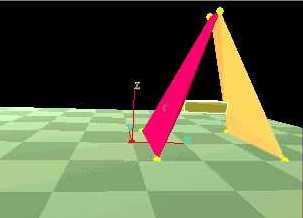
The videos below show three simulation scenes of manually-designed artifacts. On the left, a test mechanism composed of two triangular plates with a singular oscillating muscle is simulated in quasi-static motion. The motion of this test mechanism compared favorably to the physical mechanism. The two scenes on the right shows how quasi-static analysis yields pseudo-dynamic motion (even though dynamics are not accounted for in the simulation).